quarta-feira, 21 de novembro de 2012
Potenciação de Frações Algébricas
A potenciação de frações algébricas utiliza o mesmo processo das
frações numéricas, o expoente precisa ser aplicado ao numerador e ao
denominador, considerando o valor do denominador diferente de zero. Após
o desenvolvimento da potenciação, se for o caso, simplifique a fração,
pois dividindo seus elementos pelo mesmo número, isto é, pelo divisor
comum ao numerador e ao divisor. Observe alguns exemplos:
Frações Numéricas
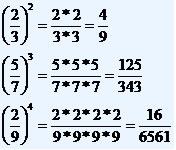
Frações Algébricas
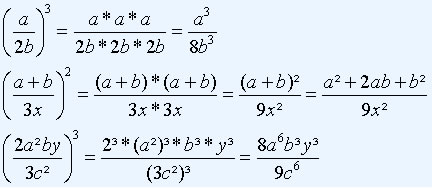
Nos casos em que o expoente possui sinal negativo, devemos inverter a base e trocar o sinal do expoente para positivo. Feito esse processo, basta aplicar o expoente ao numerador e ao denominador. Observe:
Frações Numéricas
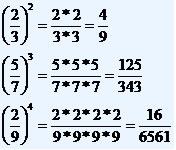
Frações Algébricas
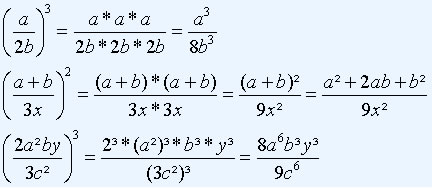
Nos casos em que o expoente possui sinal negativo, devemos inverter a base e trocar o sinal do expoente para positivo. Feito esse processo, basta aplicar o expoente ao numerador e ao denominador. Observe:

Algumas situações exigem maior complexidade nos cálculos, utilizando as
propriedades estudadas como soma de frações com denominadores
diferentes, mmc de polinômios, expoente negativo, divisão de frações,
multiplicação de frações, potenciação e simplificação de termos
semelhantes. Veja:

multiplicação e divisao de frações algébricas
Para multiplicar ou dividir frações algébricas, usamos o mesmo processo das frações numéricas. Fatorando os termos da fração e simplificar os fatores comuns.
Exemplos:



Não esqueça! Para aprender ''frações algébricas'', você precisa saber:
Polinômios
e monômios, fator comum em evidência, diferença de dois quadrados,
agrupamento, trinômio do quadrado perfeito, simplificação de frações
algébricas, operações com frações.
Exemplo de Aplicabilidade: As
expressões algébricas são encontradas muitas vezes em fórmulas
matemáticas. Por exemplo, no cálculo de áreas de retângulos, triângulos e
outras figuras planas.
adições e subtraçoes de frações algébricas
Os números na forma de fração pertencem
ao conjunto dos números racionais e são utilizados na representação das
partes de um inteiro. Entre as frações, podemos efetuar todas as
operações básicas, como adicionar, subtrair, multiplicar, dividir,
potencializar e aplicar a raiz quadrada.
Quando as frações possuem o mesmo denominador, basta somar ou subtrair os numeradores.
Ex: 

Quando as frações possuem denominadores diferentes, basta reduzi-las
ao mesmo denominador e em seguida, somar ou subtrair os numeradores.
Ex: 


Convém lembrar dos jogos de sinais.
Na expressão
( x³ + 2 y² + 1 ) – ( y ² - 2 ) = x³ +2 y² + 1 – y² + 2 = x³ + y² +3
Ex.: 2 x³ y² z + 3x³ y² z = 5x³ y² z
ou 2 x³ y² z - 3x³ y² z = -x³ y² z
Exemplos:
'.jpg)
.jpg)
Não esqueça! Para resolver '''Adição e Subtração de Frações Algébricas'', você/
Fator
comum em evidência, diferença de dois quadrados, agrupamento, trinômio
do quadrado perfeito, mmc polinômios, simpl. frações algébricas.
Exemplo de Aplicabilidade: Em
física também, bastando lembrar que no lançamento de um projétil, a
trajetória é uma parábola do segundo grau, que é um polinômio do segundo
grau (y=a.x^2+b.x+c).
SIMPLIFICAÇÃO DE FRAÇÕES ALGÉBRICAS
SIMPLIFICAÇÃO
Para simplificar uma fração, basta dividir o numerador e o denominador por seus divisores comuns.
Exemplos
1) 10 a²b / 15a³ =
(10 a a b ) / ( 15 a a a )=
( 2.5.a.a.b) /( 3.5.a.a.a) =
= 2b/3a
2) ( a² - 9) / ( a + 3) =
[(a + 3) / (a – 3) ] / (a + 3) =
= a – 3
Observe que neste último exemplo, fatoramos os termos da fração e cancelamos os termos comuns.
Uma fração que não admite mais simplificação é chamada de irredutível.
Para simplificar uma fração, basta dividir o numerador e o denominador por seus divisores comuns.
Exemplos
1) 10 a²b / 15a³ =
(10 a a b ) / ( 15 a a a )=
( 2.5.a.a.b) /( 3.5.a.a.a) =
= 2b/3a
2) ( a² - 9) / ( a + 3) =
[(a + 3) / (a – 3) ] / (a + 3) =
= a – 3
Observe que neste último exemplo, fatoramos os termos da fração e cancelamos os termos comuns.
Uma fração que não admite mais simplificação é chamada de irredutível.
FRAÇÕES ALGÉBRICAS
FRAÇÕES ALGÉBRICAS
Frações algébricas é o quociente de divisão de duas expressões algébricas
Exemplos
a) x/5y
b) (x+y) / (a – 1)
c) ( x – 1) / ( y + 2 )
Observações
1) Nas rações algébricas o numerador e o denominador são polinômios ou monômios
2) O denominador de uma fração nunca pode ser zero
3) As propriedades das frações algébricas são as mesmas das frações aritmética.
Frações algébricas é o quociente de divisão de duas expressões algébricas
Exemplos
a) x/5y
b) (x+y) / (a – 1)
c) ( x – 1) / ( y + 2 )
Observações
1) Nas rações algébricas o numerador e o denominador são polinômios ou monômios
2) O denominador de uma fração nunca pode ser zero
3) As propriedades das frações algébricas são as mesmas das frações aritmética.
agrupamento
Fatoração
Fatorar é transformar equações algébricas em produtos de duas ou mais expressões, chamadas fatores.
Fatoração por Agrupamento
Consiste em aplicar duas vezes o caso do fator comum em alguns polinômios especiais.
Como por exemplo:
ax + ay + bx + by
Os dois primeiros termos possuem em comum o fator a , os dois últimos termos possuem em comum o fator b. Colocando esses termos em evidência:
a.(x+y) + b.(x+y)
Este novo polinômio possui o termo (x+y) em comum. Assim colocando-o em evidência:
(x+y).(a+b)
Ou seja: ax + ay + bx + by = (x+y).(a+b)
Fatorar é transformar equações algébricas em produtos de duas ou mais expressões, chamadas fatores.
Fatoração por Agrupamento
Consiste em aplicar duas vezes o caso do fator comum em alguns polinômios especiais.
Como por exemplo:
ax + ay + bx + by
Os dois primeiros termos possuem em comum o fator a , os dois últimos termos possuem em comum o fator b. Colocando esses termos em evidência:
a.(x+y) + b.(x+y)
Este novo polinômio possui o termo (x+y) em comum. Assim colocando-o em evidência:
(x+y).(a+b)
Ou seja: ax + ay + bx + by = (x+y).(a+b)
fatoração-fator em evidência
Fatoração |
Página 002
|
1. Fator comum em evidência: 12x2 + 4x3 - 8x4
Nesta técnica a gente
verifica cada um dos termos, procurando ver se os
coeficientes (o que fica na na frente das variáveis x, y etc), podem ser
divididos por um certo número. Neste caso 12, +4, -8 podem ser divididos
por 4. Então, colocamos o número 4 em evidência, ou seja, antes de um
parênteses, dividimos cada um dos coeficientes por 4 e escrevemos o
resultado no lugar o próprio coeficiente. Veja:
12x2 +
4x3 - 8x4coeficientes (o que fica na na frente das variáveis x, y etc), podem ser
divididos por um certo número. Neste caso 12, +4, -8 podem ser divididos
por 4. Então, colocamos o número 4 em evidência, ou seja, antes de um
parênteses, dividimos cada um dos coeficientes por 4 e escrevemos o
resultado no lugar o próprio coeficiente. Veja:
4 (3x2 + 1x3 - 2x4). Observe que se multiplicarmos o 4 pelos novos coeficientes
3, 1 e -2 iremos ter de volta os coeficientes originais 12, 4 e -8.
1. Fator comum em evidência (Continuação)
:
12x2
+ 4x3 - 8x4 = 4
(3x2 + 1x3
- 2x4)
Agora precisamos
verificar se podemos dividir cada um dos termos que estão dentro
dos parênteses, por um mesmo fator literal (que contém letra). Neste caso podemos
notar que o fator x2 serve para dividir cada uma dos termos da expressão.
Desta forma, escrevemos o x2 antes dos parênteses, ao lado do número 4, e dividimos
cada um dos termos por ele. Veja como fica:
dos parênteses, por um mesmo fator literal (que contém letra). Neste caso podemos
notar que o fator x2 serve para dividir cada uma dos termos da expressão.
Desta forma, escrevemos o x2 antes dos parênteses, ao lado do número 4, e dividimos
cada um dos termos por ele. Veja como fica:
4x2 (3 + 1x - 2x2)
terça-feira, 28 de agosto de 2012
Produtos notáveis
A álgebra utiliza letras e números na representação de situações matemáticas. Alguns elementos, denominados produtos notáveis, são de extrema importância para o desenvolvimento de situações algébricas
Eles consistem em binômios especiais com formas de resolução através de regras matemáticas. Os produtos notáveis são conteúdos inerentes ao 8º ano do ensino fundamental e pré-requisitos para futuros conteúdos, por isso é indispensável a sua apresentação.
Apresente aos alunos os produtos notáveis seguidos de seus nomes:
(a + b)² → quadrado da soma de dois termos
(a – b)² → quadrado da diferença de dois termos
(a + b) * (a – b) → produto da soma pela diferença de dois termos
(a + b)³ → cubo da soma de dois termos
(a – b)³ → cubo da diferença de dois termos
Resolução dos produtos notáveis pela regra:
Quadrado da soma: quadrado do primeiro termo, mais duas vezes o primeiro termo vezes o segundo, mais o quadrado do segundo termo.
(a + 5)² → a² + 2 * a * 5 + 5² → a² + 10a + 25
Quadrado da diferença: quadrado do primeiro termo, menos duas vezes o primeiro termo vezes o segundo, mais o quadrado do segundo termo.
(x – 10)² → x² – 2 * x * 10 + 10² → x² – 20x + 100
Produto da soma pela diferença entre dois termos: quadrado do primeiro termo, menos o quadrado do segundo termo.
(x – 8) * (x + 8) → x² – 8² → x² – 64
Cubo da soma: cubo do primeiro termo, mais três vezes o primeiro termo elevado ao quadrado vezes o segundo termo, mais três vezes o primeiro termo vezes o segundo termo elevado ao quadrado, mais o segundo termo elevado ao cubo.
(x + 3)³ → x³ + 3 * x² * 3 + 3 * x * 3² + 3³ → x³ + 9x² + 27x + 27
Cubo da diferença: cubo do primeiro termo, menos três vezes o primeiro termo elevado ao quadrado vezes o segundo termo, mais três vezes o primeiro termo vezes o segundo termo elevado ao quadrado, menos o segundo termo elevado ao cubo.
(x – 2)² → x³ – 3 * x² * 2 + 3 * x * 2² – 2³ → x³ – 6x² + 12x – 8
Eles consistem em binômios especiais com formas de resolução através de regras matemáticas. Os produtos notáveis são conteúdos inerentes ao 8º ano do ensino fundamental e pré-requisitos para futuros conteúdos, por isso é indispensável a sua apresentação.
Apresente aos alunos os produtos notáveis seguidos de seus nomes:
(a + b)² → quadrado da soma de dois termos
(a – b)² → quadrado da diferença de dois termos
(a + b) * (a – b) → produto da soma pela diferença de dois termos
(a + b)³ → cubo da soma de dois termos
(a – b)³ → cubo da diferença de dois termos
Resolução dos produtos notáveis pela regra:
Quadrado da soma: quadrado do primeiro termo, mais duas vezes o primeiro termo vezes o segundo, mais o quadrado do segundo termo.
(a + 5)² → a² + 2 * a * 5 + 5² → a² + 10a + 25
Quadrado da diferença: quadrado do primeiro termo, menos duas vezes o primeiro termo vezes o segundo, mais o quadrado do segundo termo.
(x – 10)² → x² – 2 * x * 10 + 10² → x² – 20x + 100
Produto da soma pela diferença entre dois termos: quadrado do primeiro termo, menos o quadrado do segundo termo.
(x – 8) * (x + 8) → x² – 8² → x² – 64
Cubo da soma: cubo do primeiro termo, mais três vezes o primeiro termo elevado ao quadrado vezes o segundo termo, mais três vezes o primeiro termo vezes o segundo termo elevado ao quadrado, mais o segundo termo elevado ao cubo.
(x + 3)³ → x³ + 3 * x² * 3 + 3 * x * 3² + 3³ → x³ + 9x² + 27x + 27
Cubo da diferença: cubo do primeiro termo, menos três vezes o primeiro termo elevado ao quadrado vezes o segundo termo, mais três vezes o primeiro termo vezes o segundo termo elevado ao quadrado, menos o segundo termo elevado ao cubo.
(x – 2)² → x³ – 3 * x² * 2 + 3 * x * 2² – 2³ → x³ – 6x² + 12x – 8
Divisão de polinômios
Polinômio é uma expressão algébrica composta por dois ou mais monômios. Na divisão de polinômios, utilizamos duas regras matemáticas fundamentais: realizar a divisão entre os coeficientes numéricos e divisão de potências de mesma base (conservar a base e subtrair os expoentes).
Quando trabalhamos com divisão, utilizamos também a multiplicação no processo. Observe o seguinte esquema:
Quando trabalhamos com divisão, utilizamos também a multiplicação no processo. Observe o seguinte esquema:
.jpg)
Vamos dividir um polinômio por um monômio, com o intuito de entendermos o processo operatório. Observe:
Exemplo 1:
Exemplo 1:
.jpg)
Caso queira verificar se a divisão está correta, basta multiplicar o quociente pelo divisor, com vistas a obter o dividendo como resultado.
Verificando → quociente * divisor + resto = dividendo4x * (3x² + x – 2) + 0
12x³ + 4x² – 8x
Caso isso ocorra, a divisão está correta. No exemplo a seguir, iremos dividir polinômio por polinômio. Veja:
Verificando → quociente * divisor + resto = dividendo4x * (3x² + x – 2) + 0
12x³ + 4x² – 8x
Caso isso ocorra, a divisão está correta. No exemplo a seguir, iremos dividir polinômio por polinômio. Veja:
Multiplicação de polinômio
Multiplicação de polinômio por monômio
Para entendermos melhor, observe o exemplo:
(3x2) * (5x3 + 8x2 – x) → aplicar a propriedade distributiva da multiplicação
15x5 + 24x4 – 3x3
Multiplicação de polinômio por polinômio
Para efetuarmos a multiplicação de polinômio por polinômio também devemos utilizar a propriedade distributiva. Veja o exemplo:
(x – 1) * (x2 + 2x - 6)
x2 * (x – 1) + 2x * (x – 1) – 6 * (x – 1)
(x³ – x²) + (2x² – 2x) – (6x – 6)
x³ – x² + 2x² – 2x – 6x + 6 → reduzindo os termos semelhantes.
x³ + x² – 8x + 6
Portanto, nas multiplicações entre monômios e polinômios aplicamos a propriedade distributiva da multiplicação.
Para entendermos melhor, observe o exemplo:
(3x2) * (5x3 + 8x2 – x) → aplicar a propriedade distributiva da multiplicação
15x5 + 24x4 – 3x3
Multiplicação de polinômio por polinômio
Para efetuarmos a multiplicação de polinômio por polinômio também devemos utilizar a propriedade distributiva. Veja o exemplo:
(x – 1) * (x2 + 2x - 6)
x2 * (x – 1) + 2x * (x – 1) – 6 * (x – 1)
(x³ – x²) + (2x² – 2x) – (6x – 6)
x³ – x² + 2x² – 2x – 6x + 6 → reduzindo os termos semelhantes.
x³ + x² – 8x + 6
Portanto, nas multiplicações entre monômios e polinômios aplicamos a propriedade distributiva da multiplicação.
Adição e Subtração de um polinomio
Nas situações envolvendo cálculos algébricos, é de extrema importância a aplicação de regras nas operações entre os monômios. As situações aqui apresentadas abordarão a adição, a subtração e a multiplicação de polinômios.
Adição e Subtração
Considere os polinômios –2x² + 5x – 2 e –3x³ + 2x – 1. Vamos efetuar a adição e a subtração entre eles.
Adição
(–2x² + 5x – 2) + (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal
–2x² + 5x – 2 – 3x³ + 2x – 1 → reduzir os termos semelhantes
–2x² + 7x – 3x³ – 3 → ordenar de forma decrescente de acordo com a potência
–3x³ – 2x² + 7x – 3
Subtração
(–2x² + 5x – 2) – (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal
–2x² + 5x – 2 + 3x³ – 2x + 1 → reduzir os termos semelhantes
–2x² + 3x – 1 + 3x³ → ordenar de forma decrescente de acordo com a potência
3x³ – 2x² + 3x – 1
Adição e Subtração
Considere os polinômios –2x² + 5x – 2 e –3x³ + 2x – 1. Vamos efetuar a adição e a subtração entre eles.
Adição
(–2x² + 5x – 2) + (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal
–2x² + 5x – 2 – 3x³ + 2x – 1 → reduzir os termos semelhantes
–2x² + 7x – 3x³ – 3 → ordenar de forma decrescente de acordo com a potência
–3x³ – 2x² + 7x – 3
Subtração
(–2x² + 5x – 2) – (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal
–2x² + 5x – 2 + 3x³ – 2x + 1 → reduzir os termos semelhantes
–2x² + 3x – 1 + 3x³ → ordenar de forma decrescente de acordo com a potência
3x³ – 2x² + 3x – 1
Polinômio
Na página sobre termos algébricos explicamos o que são monômios semelhantes e em seguida tratamos a sua soma e subtração.
A adição ou subtração algébrica de monômios é denominada polinômio.
Vejamos alguns exemplos de polinômios:





No primeiro exemplo temos um polinômio de apenas um monômio. Os demais possuem vários monômios, estes monômios são denominados termos do polinômio.
O segundo exemplo é um polinômio de dois termos: 3x3y e 2xy2.
Grau de um Polinômio
O grau de um polinômio reduzido, não nulo, é o grau do seu termo de maior grau.
O polinômio -5x4 + 14x5y2 - 7x3y2 é do grau 7, pois o seu termo de maior grau é o segundo, que é do grau 7.
O polinômio 4a2b3 + 5a5 é do grau 5, pois ambos os termos do polinômio são deste grau.
Raiz quadrada
RAIZ QUADRADA
Aplicando a definição de raiz quadrada, temos:
a) √49x² = 7x, pois (7x)² = 49x²
b) √25x⁶ = 5x³, pois (5x³)² = 25x⁶
Conclusão: para extrair a raiz quadrada de um monômio, extraímos a raiz quadrada do coeficiente e dividimos o expoente de cada variável por 2
Exemplos:
a) √16x⁶ = 4x³
b) √64x⁴b² = 8x²b
Obs: Estamos admitindo que os resultados obtidos não assumam valores numéricos negativos
Aplicando a definição de raiz quadrada, temos:
a) √49x² = 7x, pois (7x)² = 49x²
b) √25x⁶ = 5x³, pois (5x³)² = 25x⁶
Conclusão: para extrair a raiz quadrada de um monômio, extraímos a raiz quadrada do coeficiente e dividimos o expoente de cada variável por 2
Exemplos:
a) √16x⁶ = 4x³
b) √64x⁴b² = 8x²b
Obs: Estamos admitindo que os resultados obtidos não assumam valores numéricos negativos
Potenciação de monômios
►Potenciação de monômios
Na potenciação de monômios devemos novamente utilizar uma propriedade da potenciação:
(I) (a . b)m = am . bm
(II) (am)n = am . n
Veja alguns exemplos:
(-5x2b6)2 aplicando a propriedade (I).
(-5)2 . (x2)2 . (b6)2 aplicando a propriedade (II)
25 . x4 . b12
25x4b12
Na potenciação de monômios devemos novamente utilizar uma propriedade da potenciação:
(I) (a . b)m = am . bm
(II) (am)n = am . n
Veja alguns exemplos:
(-5x2b6)2 aplicando a propriedade (I).
(-5)2 . (x2)2 . (b6)2 aplicando a propriedade (II)
25 . x4 . b12
25x4b12
Divisão de monômios
►Divisão de monômios
Para dividirmos os monômios não é necessário que eles sejam semelhantes, basta dividirmos coeficiente com coeficiente e parte literal com parte literal. Sendo que quando dividirmos as partes literais devemos usar a propriedade da potência que diz:
am : an = am - n (bases iguais na divisão repetimos a base e diminuímos os expoentes), sendo que a ≠ 0.
(-20x2y3) : (- 4xy3) na divisão dos dois monômios, devemos dividir os coeficientes -20 e - 4 e na parte literal dividirmos as que têm mesma base para que possamos usar a propriedade am : an = am – n.
-20 : (– 4) . x2 : x . y3 : y3
5 x2 – 1 y3 – 3
5x1y0
5x
Para dividirmos os monômios não é necessário que eles sejam semelhantes, basta dividirmos coeficiente com coeficiente e parte literal com parte literal. Sendo que quando dividirmos as partes literais devemos usar a propriedade da potência que diz:
am : an = am - n (bases iguais na divisão repetimos a base e diminuímos os expoentes), sendo que a ≠ 0.
(-20x2y3) : (- 4xy3) na divisão dos dois monômios, devemos dividir os coeficientes -20 e - 4 e na parte literal dividirmos as que têm mesma base para que possamos usar a propriedade am : an = am – n.
-20 : (– 4) . x2 : x . y3 : y3
5 x2 – 1 y3 – 3
5x1y0
5x
Multiplicação de monômios
►Multiplicação de monômios
Para multiplicarmos monômios não é necessário que eles sejam semelhantes, basta multiplicarmos coeficiente com coeficiente e parte literal com parte literal. Sendo que quando multiplicamos as partes literais devemos usar a propriedade da potência que diz:am . an = am + n (bases iguais na multiplicação repetimos a base e somamos os expoentes).
(3a2b) . (- 5ab3) na multiplicação dos dois monômios, devemos multiplicar os coeficientes 3 . (-5) e na parte literal multiplicamos as que têm mesma base para que possamos usar a propriedade am . an = am + n.
3 . ( - 5) . a2 . a . b . b3
-15 a2 +1 b1 + 3
-15 a3b4
Para multiplicarmos monômios não é necessário que eles sejam semelhantes, basta multiplicarmos coeficiente com coeficiente e parte literal com parte literal. Sendo que quando multiplicamos as partes literais devemos usar a propriedade da potência que diz:am . an = am + n (bases iguais na multiplicação repetimos a base e somamos os expoentes).
(3a2b) . (- 5ab3) na multiplicação dos dois monômios, devemos multiplicar os coeficientes 3 . (-5) e na parte literal multiplicamos as que têm mesma base para que possamos usar a propriedade am . an = am + n.
3 . ( - 5) . a2 . a . b . b3
-15 a2 +1 b1 + 3
-15 a3b4
Adição de monomios
Para iniciarmos as operações devemos saber o que são termos semelhantes.
Dizemos que um termo é semelhante do outro quando suas partes literais são idênticas. Veja:
► 5x2 e 42x são dois termos, as suas partes literais são x2 e x, as letras são iguais, mas o expoente não, então esses termos não são semelhantes.
► 7ab2 e 20ab2 são dois termos, suas partes literais são ab2 e ab2, observamos que elas são idênticas, então podemos dizer que são semelhantes.
►Adição e subtração de monômios
Só podemos efetuar a adição e subtração de monômios entre termos semelhantes. E quando os termos envolvidos na operação de adição ou subtração não forem semelhantes, deixamos apenas a operação indicada.
Veja:
Dado os termos 5xy2, 20xy2, como os dois termos são semelhantes eu posso efetuar a adição e a subtração deles.
• 5xy2 + 20xy2 devemos somar apenas os coeficientes e conservar a parte literal.
25 xy2
• 5xy2 - 20xy2 devemos subtrair apenas os coeficientes e conservar a parte literal.
- 15 xy2
Dizemos que um termo é semelhante do outro quando suas partes literais são idênticas. Veja:
► 5x2 e 42x são dois termos, as suas partes literais são x2 e x, as letras são iguais, mas o expoente não, então esses termos não são semelhantes.
► 7ab2 e 20ab2 são dois termos, suas partes literais são ab2 e ab2, observamos que elas são idênticas, então podemos dizer que são semelhantes.
►Adição e subtração de monômios
Só podemos efetuar a adição e subtração de monômios entre termos semelhantes. E quando os termos envolvidos na operação de adição ou subtração não forem semelhantes, deixamos apenas a operação indicada.
Veja:
Dado os termos 5xy2, 20xy2, como os dois termos são semelhantes eu posso efetuar a adição e a subtração deles.
• 5xy2 + 20xy2 devemos somar apenas os coeficientes e conservar a parte literal.
25 xy2
• 5xy2 - 20xy2 devemos subtrair apenas os coeficientes e conservar a parte literal.
- 15 xy2
Monômio ou termo algébrico
Definição de Monômio
Denominamos monômio ou termo algébrico quaisquer expressões algébricas representadas por um número, por uma incógnita, ou pelo produto de números e incógnitas, assim 2, x, 2x e -3xy2 são exemplos de termos algébricos ou monômios.
Identificando as Partes de um Monômio
No monômio -3xy2 o número -3 representa o seu coeficiente numérico e a sua parte literal é representada porxy2.
Por convenção omitimos o coeficiente numérico quando ele é igual a 1, escrevemos x em vez de escrevermos 1x, por exemplo, ou então -x no lugar de -1x.
Temos um monômio nulo quando o coeficiente numérico é igual a 0, assim o termo algébrico 0x2 é igual a 0.
Acima utilizamos o número 2 como um exemplo de monômio. De fato todo número real é um monômio, só que sem a parte literal.
Grau de um Monômio
O grau de um monômio é obtido através da soma dos expoentes de todas as variáveis. O coeficiente numérico deve ser diferente de zero, caso contrário o monômio será nulo.
7xy2 é um monômio de grau 3, já que o expoente de x subentende-se que seja igual a 1 e o de y é igual a 2.
O monômio -5x4 é de grau 4, pois só possui a variável x com expoente igual a 4.
182 é de grau 0, pois é um monômio sem a parte literal.
Expressões algébricas ou literais
EXPRESSÕES ALGÉBRICAS
Uma expressão matemática é denominada algébrica ou literal quando possui
“números e letras” ou explicitamente, apenas “letras”. As letras são chamadas
variáveis.
Exemplos:
a) x + y b) 3xy c) x + 4 d) 4a + 5b
1) Termo Algébrico
É todo produto indicado de números reais, representados ou não por variáveis,
pertencente a uma expressão algébrica.
Exemplos:
2xy2 + 5x3y – 10xy + 5
2xy2
→ é um termo algébrico
5x3y → é um termo algébrico
10xy → é um termo algébrico
5 → é um termo algébrico ou termo constante
Assinar:
Postagens (Atom)







