quarta-feira, 21 de novembro de 2012
Potenciação de Frações Algébricas
A potenciação de frações algébricas utiliza o mesmo processo das
frações numéricas, o expoente precisa ser aplicado ao numerador e ao
denominador, considerando o valor do denominador diferente de zero. Após
o desenvolvimento da potenciação, se for o caso, simplifique a fração,
pois dividindo seus elementos pelo mesmo número, isto é, pelo divisor
comum ao numerador e ao divisor. Observe alguns exemplos:
Frações Numéricas
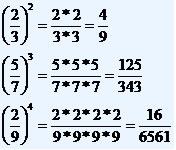
Frações Algébricas
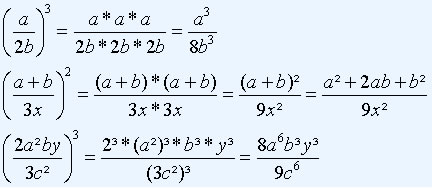
Nos casos em que o expoente possui sinal negativo, devemos inverter a base e trocar o sinal do expoente para positivo. Feito esse processo, basta aplicar o expoente ao numerador e ao denominador. Observe:
Frações Numéricas
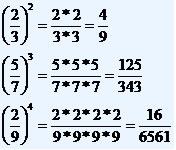
Frações Algébricas
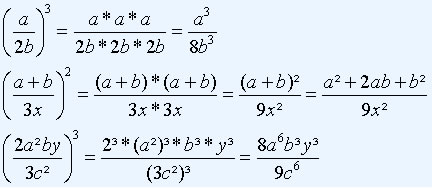
Nos casos em que o expoente possui sinal negativo, devemos inverter a base e trocar o sinal do expoente para positivo. Feito esse processo, basta aplicar o expoente ao numerador e ao denominador. Observe:

Algumas situações exigem maior complexidade nos cálculos, utilizando as
propriedades estudadas como soma de frações com denominadores
diferentes, mmc de polinômios, expoente negativo, divisão de frações,
multiplicação de frações, potenciação e simplificação de termos
semelhantes. Veja:

multiplicação e divisao de frações algébricas
Para multiplicar ou dividir frações algébricas, usamos o mesmo processo das frações numéricas. Fatorando os termos da fração e simplificar os fatores comuns.
Exemplos:



Não esqueça! Para aprender ''frações algébricas'', você precisa saber:
Polinômios
e monômios, fator comum em evidência, diferença de dois quadrados,
agrupamento, trinômio do quadrado perfeito, simplificação de frações
algébricas, operações com frações.
Exemplo de Aplicabilidade: As
expressões algébricas são encontradas muitas vezes em fórmulas
matemáticas. Por exemplo, no cálculo de áreas de retângulos, triângulos e
outras figuras planas.
adições e subtraçoes de frações algébricas
Os números na forma de fração pertencem
ao conjunto dos números racionais e são utilizados na representação das
partes de um inteiro. Entre as frações, podemos efetuar todas as
operações básicas, como adicionar, subtrair, multiplicar, dividir,
potencializar e aplicar a raiz quadrada.
Quando as frações possuem o mesmo denominador, basta somar ou subtrair os numeradores.
Ex: 

Quando as frações possuem denominadores diferentes, basta reduzi-las
ao mesmo denominador e em seguida, somar ou subtrair os numeradores.
Ex: 


Convém lembrar dos jogos de sinais.
Na expressão
( x³ + 2 y² + 1 ) – ( y ² - 2 ) = x³ +2 y² + 1 – y² + 2 = x³ + y² +3
Ex.: 2 x³ y² z + 3x³ y² z = 5x³ y² z
ou 2 x³ y² z - 3x³ y² z = -x³ y² z
Exemplos:
'.jpg)
.jpg)
Não esqueça! Para resolver '''Adição e Subtração de Frações Algébricas'', você/
Fator
comum em evidência, diferença de dois quadrados, agrupamento, trinômio
do quadrado perfeito, mmc polinômios, simpl. frações algébricas.
Exemplo de Aplicabilidade: Em
física também, bastando lembrar que no lançamento de um projétil, a
trajetória é uma parábola do segundo grau, que é um polinômio do segundo
grau (y=a.x^2+b.x+c).
SIMPLIFICAÇÃO DE FRAÇÕES ALGÉBRICAS
SIMPLIFICAÇÃO
Para simplificar uma fração, basta dividir o numerador e o denominador por seus divisores comuns.
Exemplos
1) 10 a²b / 15a³ =
(10 a a b ) / ( 15 a a a )=
( 2.5.a.a.b) /( 3.5.a.a.a) =
= 2b/3a
2) ( a² - 9) / ( a + 3) =
[(a + 3) / (a – 3) ] / (a + 3) =
= a – 3
Observe que neste último exemplo, fatoramos os termos da fração e cancelamos os termos comuns.
Uma fração que não admite mais simplificação é chamada de irredutível.
Para simplificar uma fração, basta dividir o numerador e o denominador por seus divisores comuns.
Exemplos
1) 10 a²b / 15a³ =
(10 a a b ) / ( 15 a a a )=
( 2.5.a.a.b) /( 3.5.a.a.a) =
= 2b/3a
2) ( a² - 9) / ( a + 3) =
[(a + 3) / (a – 3) ] / (a + 3) =
= a – 3
Observe que neste último exemplo, fatoramos os termos da fração e cancelamos os termos comuns.
Uma fração que não admite mais simplificação é chamada de irredutível.
FRAÇÕES ALGÉBRICAS
FRAÇÕES ALGÉBRICAS
Frações algébricas é o quociente de divisão de duas expressões algébricas
Exemplos
a) x/5y
b) (x+y) / (a – 1)
c) ( x – 1) / ( y + 2 )
Observações
1) Nas rações algébricas o numerador e o denominador são polinômios ou monômios
2) O denominador de uma fração nunca pode ser zero
3) As propriedades das frações algébricas são as mesmas das frações aritmética.
Frações algébricas é o quociente de divisão de duas expressões algébricas
Exemplos
a) x/5y
b) (x+y) / (a – 1)
c) ( x – 1) / ( y + 2 )
Observações
1) Nas rações algébricas o numerador e o denominador são polinômios ou monômios
2) O denominador de uma fração nunca pode ser zero
3) As propriedades das frações algébricas são as mesmas das frações aritmética.
agrupamento
Fatoração
Fatorar é transformar equações algébricas em produtos de duas ou mais expressões, chamadas fatores.
Fatoração por Agrupamento
Consiste em aplicar duas vezes o caso do fator comum em alguns polinômios especiais.
Como por exemplo:
ax + ay + bx + by
Os dois primeiros termos possuem em comum o fator a , os dois últimos termos possuem em comum o fator b. Colocando esses termos em evidência:
a.(x+y) + b.(x+y)
Este novo polinômio possui o termo (x+y) em comum. Assim colocando-o em evidência:
(x+y).(a+b)
Ou seja: ax + ay + bx + by = (x+y).(a+b)
Fatorar é transformar equações algébricas em produtos de duas ou mais expressões, chamadas fatores.
Fatoração por Agrupamento
Consiste em aplicar duas vezes o caso do fator comum em alguns polinômios especiais.
Como por exemplo:
ax + ay + bx + by
Os dois primeiros termos possuem em comum o fator a , os dois últimos termos possuem em comum o fator b. Colocando esses termos em evidência:
a.(x+y) + b.(x+y)
Este novo polinômio possui o termo (x+y) em comum. Assim colocando-o em evidência:
(x+y).(a+b)
Ou seja: ax + ay + bx + by = (x+y).(a+b)
fatoração-fator em evidência
Fatoração |
Página 002
|
1. Fator comum em evidência: 12x2 + 4x3 - 8x4
Nesta técnica a gente
verifica cada um dos termos, procurando ver se os
coeficientes (o que fica na na frente das variáveis x, y etc), podem ser
divididos por um certo número. Neste caso 12, +4, -8 podem ser divididos
por 4. Então, colocamos o número 4 em evidência, ou seja, antes de um
parênteses, dividimos cada um dos coeficientes por 4 e escrevemos o
resultado no lugar o próprio coeficiente. Veja:
12x2 +
4x3 - 8x4coeficientes (o que fica na na frente das variáveis x, y etc), podem ser
divididos por um certo número. Neste caso 12, +4, -8 podem ser divididos
por 4. Então, colocamos o número 4 em evidência, ou seja, antes de um
parênteses, dividimos cada um dos coeficientes por 4 e escrevemos o
resultado no lugar o próprio coeficiente. Veja:
4 (3x2 + 1x3 - 2x4). Observe que se multiplicarmos o 4 pelos novos coeficientes
3, 1 e -2 iremos ter de volta os coeficientes originais 12, 4 e -8.
1. Fator comum em evidência (Continuação)
:
12x2
+ 4x3 - 8x4 = 4
(3x2 + 1x3
- 2x4)
Agora precisamos
verificar se podemos dividir cada um dos termos que estão dentro
dos parênteses, por um mesmo fator literal (que contém letra). Neste caso podemos
notar que o fator x2 serve para dividir cada uma dos termos da expressão.
Desta forma, escrevemos o x2 antes dos parênteses, ao lado do número 4, e dividimos
cada um dos termos por ele. Veja como fica:
dos parênteses, por um mesmo fator literal (que contém letra). Neste caso podemos
notar que o fator x2 serve para dividir cada uma dos termos da expressão.
Desta forma, escrevemos o x2 antes dos parênteses, ao lado do número 4, e dividimos
cada um dos termos por ele. Veja como fica:
4x2 (3 + 1x - 2x2)
Assinar:
Postagens (Atom)







